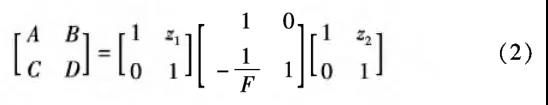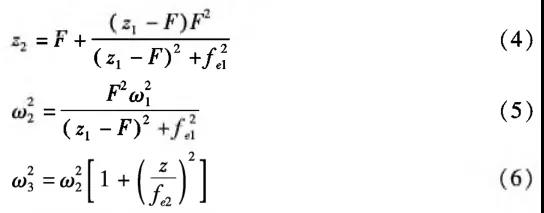In general, the irradiation intensity of laser is Gaussian, and in the process of laser use, optical system is usually used to transform the beam accordingly.

Different from the linear theory of geometric optics, the optical transformation theory of Gaussian beam is nonlinear, which is closely related to the parameters of laser beam itself and the relative position of optical system.

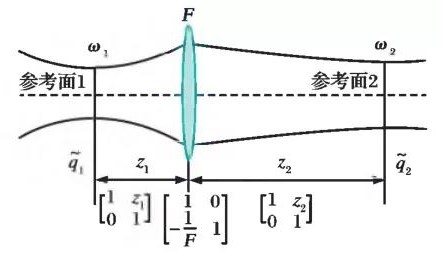
There are many parameters to describe the Gaussian laser beam, but the relationship between the spot radius and the beam waist position is often used in solving practical problems. That is, the waist radius of the incident beam (ω₁) and the distance of the optical transformation system (z₁) are known, and then the transformed beam waist radius (ω₂), beam waist position (z₂) and the spot radius (ω₃) at any position (z) are obtained. Focus on the lens, and select the front and rear waist positions of the lens as reference plane 1 and reference plane 2 respectively, as shown in Fig. 1.

                     Fig. 1 Transformation of Gauss through thin lens

According to the parameter q theory of Gaussian beam, the q₁ and q₂ on the two reference planes can be expressed as:

In the above formula: The f_e1 and f_e2 are respectively the confocus parameters before and after Gaussian beam transformation. After the Gaussian beam passes through the free space z₁, the thin lens with focal length F and the free space z₂, according to the ABCD transmission matrix theory, the following can be obtained:

Meanwhile, q₁ and q₂ satisfy the following relationships:

By combining the above formulas and making the real and imaginary parts at both ends of the equation equal respectively, we can get:

Equations (4) – (6) are the transformation relationship between the waist position and the spot size of the Gaussian beam after passing through the thin lens.